optimizacion

OPTIMIZACIÓN 1

En matemáticas la optimización o programación matemática intenta dar respuesta a un tipo general de problemas donde se desea elegir el mejor entre un conjunto de elementos. En su forma más simple, el problema equivale a resolver una ecuación de este tipo:

Donde x = (x₁,...,x_n) es un vector y representa variables de decisión, f(x) es llamada función objetivo y representa o mide la calidad de las decisiones (usualmente números enteros o reales) y Ω es el conjunto de puntos o decisiones factibles o restricciones del problema.
Algunas veces es posible expresar el conjunto de restricciones Ω como solución de un sistema de igualdades o desigualdades.

Un problema de optimización trata entonces de tomar una decisión óptima para maximizar (ganancias, velocidad, eficiencia, etc.) o minimizar un criterio determinado (costos, tiempo, riesgo, error, etc). Las restricciones significan que no cualquier decisión es posible.


EJEMPLO
El beneficio neto mensual, en millones de euros, de una empresa que fabrica autobuses viene dado por la función:

B(x)= 1.2x − (0.1x)³

donde x es el número de autobuses fabricados en un mes.

1. Calcula la producción mensual que hacen máximo el beneficio.

2. El beneficio máximo correspondiente a dicha producción.

opttimización 2

De todos los triángulos isósceles de 12 m de perímetro, hallar los lados del que tome área máxima.

La función que tenemos que maximizar es el área del triángulo:

Relacionamos las variables:

2x + 2y = 12

x = 6 − y

Sustituimos en la función:

Derivamos, igualamos a cero y calculamos las raíces.

Realizamos la 2ª derivada y sustituimos por 2, ya que la solución y = 0 la descartamos porque no hay un triángulo cuyo lado sea cero.

Por lo que queda probado que en y = 2 hay un máximo.

La base (2y) mide 4m y los lados oblicuos (x) también miden 4 m, por lo que el triangulo de área máxima sería un triangulo equilatero.

puntos críticos: máximos, mínimos, inflexión

Máximos de una Función.

En un punto en el que la derivada se anule y antes sea positiva y después del punto negativa, se dice que la función tiene un máximo relativo. Es decir, que F'(xo) = 0 y en ese punto, la función, pase de creciente a decreciente. En x = a la función tiene un máximo relativo y se observa que su derivada se anula en ese punto, pasando de positiva a negativa. (se anula y cambia de signo). Máx en (a,f(a))

Mínimos de una Función.
En un punto en el que la derivada se anule y antes sea negativa y después del punto positiva, se dice que la función tiene un mínimo relativo. Es decir, que F'(xo) = 0 y en ese punto, la función, pase de decreciente a creciente. En x = b la función tiene un mínimo relativo y se observa que su derivada se anula en ese punto, pasando de negativa a positiva. Mín en (b,f(b).
Para que una función tenga máximo o mínimo no es suficiente con que su derivada se anule (debe, además, cambiar de signo).

Punto de inflexión
Un punto de inflexión es aquel donde la función derivada tiene un máximo o mínimo, es decir, un punto singular. Se dice que la función tiene un cambio en la concavidad.
Para calcular los puntos de inflexión hay que igualar a cero la derivada segunda y comprobar que ésta cambia de signo. Es decir, estudiar los máximos y mínimos de la primera derivada, para ello se deriva la primera derivada (segunda derivada) y se anula. En los puntos donde la segunda derivada se anule y cambie de signo, la función tendrá un punto de inflexión y su derivada un máx. o un mín. En la gráfica, en x = 0 la función tiene un punto de inflexión y en el su derivada tiene un mínimo en (0,c).
Donde la derivada segunda sea positiva se dice que la función es cóncava positiva y donde es negativa concavidad negativa. Un punto de inflexión es donde la función cambia de concavidad.

En F(x) = x4 - 4•x2 = x2•(x2 - 1) puede observarse que su derivada:
F'(x) = 4•x3 - 8•x = 4•x•(x2 - 2) presenta un máximo y un míninimo en x = ± √(2/3). Es aquí donde la función presenta puntos de inflexión.


Función creciente y/o decreciente.

Creciente en xo si para x > xo F(x) ≥ F(xo) ► F ' (xo) ≥ 0

ya que:

F(x) - F(xo)


F'(xo) = Lim
————————

≥ 0
x → xo
x - xo



Una función F(x) se dice que es Creciente en un punto, xo, si su derivada, en ese punto, xo, es positiva; F '(xo) ≥ 0. En la gráfica se puede ver que esto ocurre desde -∞ hasta a y desde b hasta +∞. En esos intervalos la derivada (pendiente) está por encima del ejes X (es positiva).

Decreciente en xo si para x > xo F(x) ≤ F(xo) ► F ' (xo) ≤ 0

Una función F(x) se dice que es Decreciente en un punto, xo, si su derivada, en ese punto, xo, es negativa; F '(xo) ≤ 0. En la gráfica se observa que esto ocurre para valores de x comprendidos entre a y b. En este intervalo la derivada está por debajo del eje X (es negativa)

.

Criterio de la segunda derivada

Uno de los ordenes de derivación es el de la segunda derivada, aunque no es despreciable la utilización de las derivadas de orden superior, sobre todo en cálculo de errores. Curiosamente las aplicaciones físicas implican, por lo general, derivadas de segundo orden como podría ser las ecuaciones de movimiento.

 

En esta sección presentaremos una interpretación gráfica de los criterios de la segunda derivada que nos servirá para poder obtener los máximos o mínimos de una función. Antes de analizar como es la relación de la segunda derivada conoceremos algunas definiciones:

 

Definición.

Cóncava hacia abajo. Se dice que una función es  cóncava  hacia abajo cuando la primera derivada es  creciente en un intervalo abierto (a,b)

 

 

 

Definición.

Puntos de inflexión y número de inflexión. Sea f una función y a un número. Supongamos que existe números b y c tales que b<a<c  y además:

a)      f es una función continua en el intervalo abierto (b,c)

b)      f es una función cóncava hacia arriba y cóncava hacia abajo en (a,c), o viceversa.

 

Bajo las condiciones anteriores el punto (a,f(a)) se llama punto de inflexión, y al número a se llama número de inflexión.

 

Si la segunda derivada f´´ de una función f es positiva en un intervalo abierto (a,b) es porque la primera derivada f´ es creciente en ese  intervalo.

 

 

 

 

 

 

 

 

Criterios de la segunda derivada para máximos y mínimos relativos

 

 

Sea f una función con su primera derivada definida, al menos, en un intervalo abierto conteniendo al número a. Si f´´ esta definida entonces podemos considerar los siguiente aspectos:

 

a).-  Si f´(a)=0   y     f´´(a)<0 entonces se dice que f tiene un máximo local en a.

b).- Si f´(a)=0    y    f´(a)>0 entonces se dice que f tiene un mínimo local en a.

criterio de la primera derivada

La base del presente criterio radica en observar que los máximos o mínimos locales son consecuencia de observar los siguientes hechos:   1.- Cuando la derivada es positiva la función crece. 2.- Cuando la derivada es negativa la función decrece. 3.- Cuando la derivada es cero la función tiene un máximo o un mínimo.   Sea f(x) una función y c un número en su dominio. Supongamos que existe a y b  con a<c<b tales que   1.-  f es continua en el intervalo abierto (a,b) (de acuerdo con el teorema de Rolle) 2.- f es derivable en el intervalo abierto (a,b), excepto quizá en c; 3.- f´(x) es positiva para todo x<c en el intervalo y negativa para todo x>c en el intervalo.   Entonces f tiene un máximo local en c.   Nótese que un criterio similar puede tenerse para obtener un mínimo local, solo es necesario intercambiar  “positivo”  por “negativo”.       De manera intuitiva podemos observar que para determinar si existe un máximo o un mínimo  basta graficar alrededor de los puntos donde se ha presentado un cambio de signo Es también importante tener en consideración que el termino alrededor del cambio de signo de la derivada de la función es muy relativo y es este punto donde tenemos que tener la máxima consideración. Un punto mas a considerar es el tener en cuenta que solo es necesario considerar no solo el cambio de signos para la derivada Por ejemplo, para el caso de la función:   la función entre el intervalo (-1,1) tiene un cambio de signo, sin embargo, la función no es diferenciable en el punto x = 0, pese a eso si existe un mínimo local.

derivacion en cadena

Derivación en Cadena

Descripción de la regla

En términos intuitivos, si una variable y, depende de una segunda variable u, que a la vez depende de una tercera variable x; entonces, la razón de cambio de y con respecto a x puede ser computado como el producto de la razón de cambio de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.

Descripción algebraica

En boxes los términos algebraicos, la regla de la cadena (para funciones de una variable) afirma que si es diferenciable en y es una función diferenciable en , entonces la función compuesta 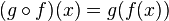es diferenciable en y

Notación de Leibniz

Alternativamente, en la notación de Leibniz, la regla de la cadena puede expresarse como:

donde indica que g depende de f como si ésta fuera una variable.

Ejemplo conceptual

Supóngase que se está escalando una montaña a una razón de 0,5 kilómetros por hora. La razón a la cual la temperatura decrece es 6 °F por kilómetro (la temperatura es menor a elevaciones mayores). Al multiplicar 6 °F por kilómetro y 0,5 kilómetros por hora, se obtiene 3 °F por hora, es decir, la razón de cambio de temperatura con respecto al tiempo transcurrido.

Este cálculo es una aplicación típica de la regla de la cadena.

Ejemplo algebraica

Por ejemplo si y = f(u) es una función derivable de u y si además u = g(x) es una función derivable de x entonces y = f(g(x)) es una función derivable con:

o también

Ejemplo 1

y queremos calcular:

Por un lado tenemos:

y

si:

entonces:

Si definimos como función de función:

resulta que:

con el mismo resultado.

Derivación implícita

Es posible derivar una función dada implícitamente sin necesidad de expresarlo explícitamente. El método consiste en derivar los dos miembros de la relación. El procedimiento se conoce como derivación implícita.

Definición: se denomina función implícita cuando se da una relación entrex yy por medio de una ecuación no resuelta paray, entoncesy se llama función implícita dex.

.

tipos de derivadas

Aquí voy a explicar un poco los diferentes casos de las derivas.

La derivada de una función constante: es cero (0).

Ejm:

1)f (x)=4

f  ´(x)=0

2)f (x)=123

f  ´(x)=0

Derivada exponencial: Es igual al exponente por la variable elevado a una unidad menos.

Ejm:

1)f(x)= 5x³

f´(x)= 3*5x^3-1

f´(x)=15x²

2)f(x)= 2x⁵⁶²

f´(x)= 562*2x^562-1

f´(x)=1124x⁵⁶¹

Derivada de una raíz: Es colocar el índice de la raíz como denominador de una función exponencial y se resuelve como si fuera una derivada de tipo exponencial y se multiplica por la derivada de la base.

Ejm:

y= Raíz cubica de x⁵  ---------------   x^5/3

y´= 5/3*x^5/3-1*1(Uno es la derivada de la base).

Derivada del cociente de dos funciones es igual a la derivada del numerador por el denominador menos la derivada del denominador por el numerador, divididas por el cuadrado del denominador.

Y=u/v^{32.-­­­­­­­­­-}-------------------- y´= u´*v-u*v´/v²

·         y= (5x²-x)/ (3x⁴-2)

y´= (10x-1)*(3x⁴-2)-(5x²-x)*(12x³)/(3x⁴-2)² R/

·         y= (3x²+4)³/(5x³-x)

y´=3(x²+4)²(6x)*(5x³-x)-( 3x²+4)³*(15x²-1)/(5x³-x)²

Derivación en cadena: Sea f(x)= f(g(x)) ­­­­­­­­­­­­­­­­­­^{________________}f´(x)=f´(g(x))*g´(x)

y= Raíz cuadrada de 3x²-1

y= (3x²-1)^1/2

y= ½(3x²-1)^1/2-1*6x

y= 3x*(3x²-1)^1/2

SOLUCION PROBLEMA